
作者: Acquired 時(shí)間: 2025-3-22 14:52

作者: Acquired 時(shí)間: 2025-3-22 19:28

作者: 斗志 時(shí)間: 2025-3-22 21:31

作者: 臆斷 時(shí)間: 2025-3-23 01:27
General Classes of Degenerate Elliptic Differential Operators,ifferent types of operators and spaces. Operators of Type 1 are hypoelliptic in the sense of the calculus of Section 1.2 up to Γ. We study these operators like we did in Section 2.2. The new elements in our consideration are introduction of the set of matrix boundary symbols, the invertibility of wh
作者: ASSET 時(shí)間: 2025-3-23 07:13
Algebra of Boundary Value Problems for Class of Pseudodifferential Operators which Change Order on wBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr% pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs% 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai% aabeqaamaabaabauaakeaacuWIDesOgaqeamaaDaaaleaacqGHRaWk% aeaacaWGUbaaaa
作者: 背帶 時(shí)間: 2025-3-23 13:37
Spectral Asymptotics of Hypoelliptic Operators with Multiple Characteristics,k.) lie on a convex broken line (or an interval) . with the vertices at the points .% MathType!MTEF!2!1!+-% feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-
作者: 假裝是你 時(shí)間: 2025-3-23 16:46
https://doi.org/10.1007/978-3-540-71283-1 .. into ... The norm of . ∈ .(.., ..) is denoted by ‖. : .. → .‖. The group of operators in ., with bounded inverses, is denoted by . and the unit of the algebra ..= .. is denoted by .% MathType!MTEF!2!1!+-% feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDY
作者: 心胸開(kāi)闊 時(shí)間: 2025-3-23 18:35
https://doi.org/10.1007/978-3-540-71283-1 degenerates on Г into a lower order operator with respect to at least some of derivatives. To describe the character of degeneracy of ., consider a small . — neighbourhood .. of the boundary Г as Г × (0, .); let .. be the coordinate along the normal to Г and let . be local coordinates on Г. We will
作者: 蛛絲 時(shí)間: 2025-3-24 02:00
https://doi.org/10.1007/978-3-540-71283-1ifferent types of operators and spaces. Operators of Type 1 are hypoelliptic in the sense of the calculus of Section 1.2 up to Γ. We study these operators like we did in Section 2.2. The new elements in our consideration are introduction of the set of matrix boundary symbols, the invertibility of wh
作者: Chronic 時(shí)間: 2025-3-24 06:15
https://doi.org/10.1007/978-3-540-71283-1wBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr% pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs% 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai% aabeqaamaabaabauaakeaacuWIDesOgaqeamaaDaaaleaacqGHRaWk% aeaacaWGUbaaaa
作者: FLIP 時(shí)間: 2025-3-24 08:57
https://doi.org/10.1007/978-3-540-71283-1k.) lie on a convex broken line (or an interval) . with the vertices at the points .% MathType!MTEF!2!1!+-% feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-
作者: STELL 時(shí)間: 2025-3-24 11:57

作者: 溫和女孩 時(shí)間: 2025-3-24 15:08

作者: 最小 時(shí)間: 2025-3-24 20:37

作者: 消音器 時(shí)間: 2025-3-25 00:59
978-90-481-4282-8Springer Science+Business Media B.V. 1993
作者: conifer 時(shí)間: 2025-3-25 07:25

作者: Temporal-Lobe 時(shí)間: 2025-3-25 08:48
https://doi.org/10.1007/978-3-540-71283-1As we noted in Subsection 2.1.3, operators of Type 1 are included in the algebra of .do with double symbols and all the results of Subsections 1.2.4 – 1.2.6 are applicable. Clearly, the same can be obtained when the functions which determine the degeneration are of non — power type. For an example, see Example 1.2.6.5.
作者: enflame 時(shí)間: 2025-3-25 14:25

作者: CLOWN 時(shí)間: 2025-3-25 18:15

作者: 聰明 時(shí)間: 2025-3-25 21:34

作者: 多樣 時(shí)間: 2025-3-26 00:47
https://doi.org/10.1007/978-3-540-71283-1First, we cite several well — known facts concerning quadratic forms in a Hilbert space . (see, for example, Chapter 6 in Kato [1]).
作者: 幼稚 時(shí)間: 2025-3-26 06:04
https://doi.org/10.1007/978-3-540-71283-1Let . be one of the forms introduced in Chapter 6 and let .and .. be the same as in Subsection 3.1.2. Let either . satisfy the conditions of one of Theorems 6.2.1.1, 6.3.1.1, 6.4.1.1 and . or let . satisfy the conditions of Theorem 6.3.1.2 and . denote by . the operator associated with the variational triple .,., ..(Ω; ?.).
作者: Maximizer 時(shí)間: 2025-3-26 09:15
Introduction,The partial differential equation.is called elliptic on a set ., provided that the principal symbol.of the operator . is invertible on . × (?. 0); . is called elliptic on ., too. This definition works for systems of equations, for classical pseudodifferential operators (.do), and for operators on a manifold Ω.
作者: circuit 時(shí)間: 2025-3-26 15:53
,Degenerate Elliptic Operators in Non — Power — Like Degeneration Case,As we noted in Subsection 2.1.3, operators of Type 1 are included in the algebra of .do with double symbols and all the results of Subsections 1.2.4 – 1.2.6 are applicable. Clearly, the same can be obtained when the functions which determine the degeneration are of non — power type. For an example, see Example 1.2.6.5.
作者: restrain 時(shí)間: 2025-3-26 18:13
,,, — Theory for Degenerate Elliptic Operators,We develop one of the simplest theories which suffices to study degenerate elliptic operators in scales of weighted Sobolev spaces based on .., 1 < . < ∞.
作者: 感激小女 時(shí)間: 2025-3-26 21:37

作者: aggressor 時(shí)間: 2025-3-27 02:15
Some Classes of Hypoelliptic Pseudodifferential Operators on Closed Manifold,The results of this section are well — known. See, for instance H?rmander [7].
作者: entitle 時(shí)間: 2025-3-27 07:31

作者: Aqueous-Humor 時(shí)間: 2025-3-27 12:20
Spectral Asymptotics of Degenerate Elliptic Operators,Let . be one of the forms introduced in Chapter 6 and let .and .. be the same as in Subsection 3.1.2. Let either . satisfy the conditions of one of Theorems 6.2.1.1, 6.3.1.1, 6.4.1.1 and . or let . satisfy the conditions of Theorem 6.3.1.2 and . denote by . the operator associated with the variational triple .,., ..(Ω; ?.).
作者: 概觀 時(shí)間: 2025-3-27 16:17
作者: 小卒 時(shí)間: 2025-3-27 18:52
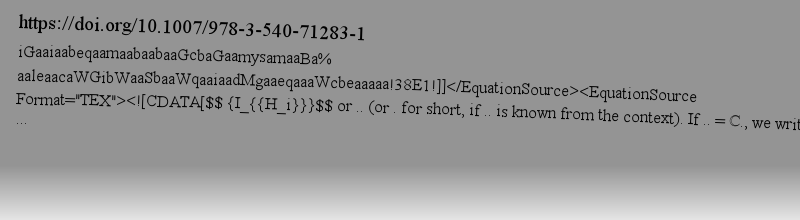
General Calculus of Pseudodifferential Operators,iGaaiaabeqaamaabaabaaGcbaGaamysamaaBa% aaleaacaWGibWaaSbaaWqaaiaadMgaaeqaaaWcbeaaaaa!38E1!]]
